Problema 108-9    Fuente: Ejemplo 9.2 - Máquinas eléctricas - Umans, Stephen & Fitzgerald - 7.ª edición - McGraw Hill Education - 2014

Un motor de 1/4 hp, 110 V, 60 Hz, de 4 polos y arranque por condensador tiene los siguientes parámetros de circuito equivalentes:

R₁ = 2,02 Ω  R₂ = 4,12 Ω   X₁ = 2,79 Ω   X₂ = 2,12 Ω   y   X_m = 66,8 Ω  

El motor funciona a tensión y frecuencia nominales con el devanado auxiliar abierto. Sabiendo que las pérdidas en el núcleo son de 24 W, las pérdidas rotacionales de 13 W y el deslizamiento s = 0,05, determine:

a) la corriente del estator;

b) el factor de potencia, FP, del motor;

c) la potencia nominal;

d) la velocidad angular síncrona;

e) el par en el eje del motor;

f) la eficiencia de la máquina.

Solución del Problema 108-9   

Item a

Para calcular la corriente del estator, primero debemos hallar el valor de impedancia total que el circuito ofrece a la fuente de tensión. Para ello, debemos hallar las impedancias de los campos directo e inverso. Utilizaremos las ecuaciones aproximadas desarrolladas en la sección teórica. Para hallar la impedancia del campo directo, utilizamos las ecuaciones eq.108-7a e eq.108-7b, repetido a continuación.

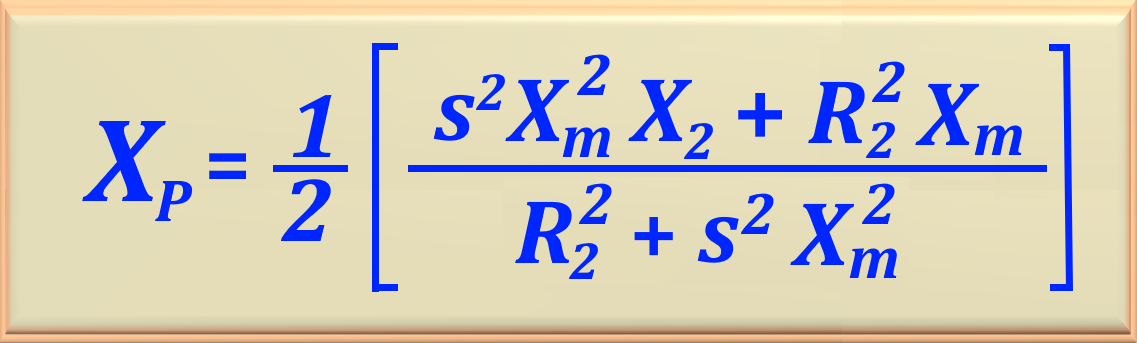
Utilizando los datos del problema, reemplazando las variables con sus respectivos valores numéricos y realizando el cálculo, encontramos:

Por lo tanto, la impedancia progresiva es:

Ahora debemos calcular la impedancia inversa. Para ello, utilizaremos las ecuaciones eq.108-8a y eq.108-8b que se muestran a continuación.

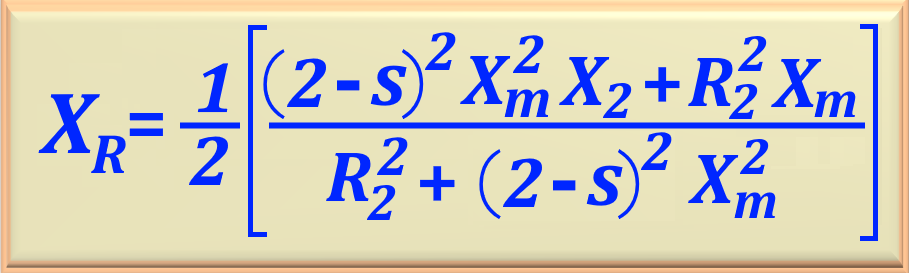
Utilizando los datos del problema y reemplazando las variables con sus respectivos valores y realizando el cálculo, encontramos:

Por lo tanto, la impedancia retrógrada es:

Luego de estos cálculos es posible calcular el valor de la impedancia total del circuito, es decir:

Utilizando los valores calculados, sustituyéndolos en la ecuación anterior y realizando el cálculo, encontramos:

Ahora podemos calcular la corriente que fluye a través del devanado del estator.

Realizando el cálculo encontramos:

Item b

Para calcular el factor de potencia, simplemente utilice el ángulo de corriente del estator, ya que adoptamos un ángulo cero-x para la tensión. Dado que la impedancia del motor es predominantemente inductiva, el factor de potencia está en atraso, o:

Item c

Para encontrar la potencia nominal, calcularemos la potencia del entrehierro utilizando la eq. 108-13, que se repite a continuación.

Reemplazando las variables por sus respectivos valores numéricos y realizando el cálculo, encontramos:

Con el valor de la potencia en el entrehierro, podemos calcular el valor de la potencia mecánica utilizando la eq. 108-27, que se muestra a continuación.

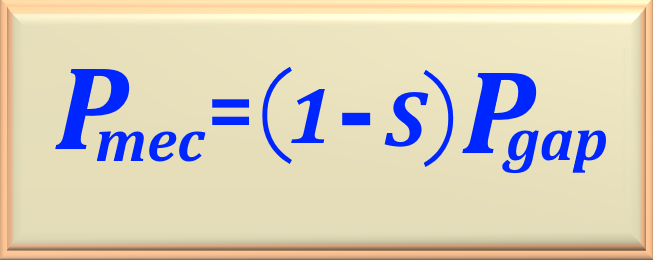
Por lo tanto, sustituyendo las variables por sus respectivos valores numéricos y realizando el cálculo, encontramos:

Para encontrar la potencia nominal debemos restar a la potencia mecánica las pérdidas mencionadas en el problema, es decir:

Item d

Para encontrar la velocidad angular sincrónica utilizaremos la eq. 108-14 que se muestra a continuación.

Por lo tanto, sustituyendo las variables por sus respectivos valores numéricos y realizando el cálculo, encontramos:

Item e

Para calcularmos o torque no eixo do motor devemos conhecer a velocidade angular do rotor, ou:

Luego, utilizando la eq. 108-17 que se muestra a continuación.

Por lo tanto, sustituyendo las variables por sus respectivos valores numéricos y realizando el cálculo, encontramos:

Item f

Para encontrar la eficiencia de la máquina, calcularemos la potencia de entrada, P_ele, utilizando la eq. 108-29, que se muestra a continuación.

Entonces, reemplazando las variables con sus respectivos valores numéricos y realizando el cálculo, encontramos:

Ahora, utilizando la ecuación eq. 108-31, el rendimiento será:

Equilibrio de Potencia

Comprobemos si las potencias implicadas en el problema cumplen con la conservación de la energía. La potencia disipada en R₁, R_P y R_R son:

Sumando estas tres potencias, obtenemos P_suma = 61,15 W. A este valor debemos sumarle la constante de pérdidas del enunciado del problema. Por lo tanto:

También podemos calcular las pérdidas totales de la máquina haciendo:

Tenga en cuenta que esta pequeña diferencia de 2 W se encuentra dentro del margen de tolerancia. Todos los resultados de los cálculos realizados con nuestras ecuaciones aproximadas, según la parte teórica, coincidieron plenamente con los resultados obtenidos en el libro de referencia.