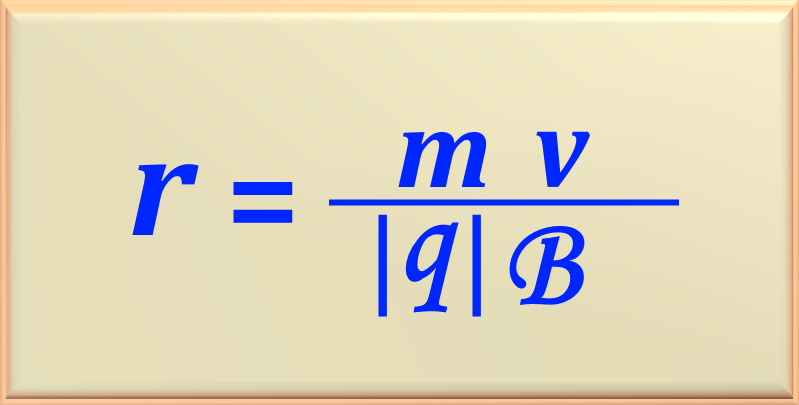Problema 74-1
Fonte: Problema elaborado pelo autor do site
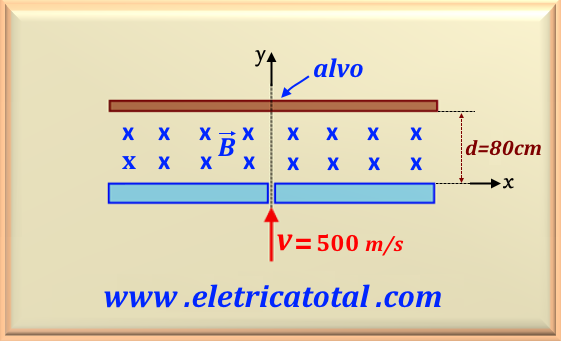
Uma partícula carregada positivamente, conforme mostra a Figura 74-01.1, com massa igual a
m = 5 x 10-7 Kg e carga igual
a q = 10-4 C, ao passar por um orifício de um anteparo, penetra em um ambiente que
está sob a ação de um campo indução magnético de B = 2,5 T com orientação penetrando na página. Paralelamente ao anteparo,
existe um alvo que dista 80 cm do anteparo. Se ao atravessar o orifício a partícula possui
uma velocidade de v = 500 m/s, determine:
a) a que distância lateral em relação ao orifício, a partícula colidirá com o alvo?
b) a trajetória da partícula (mostre através de um diagrama).
Conforme foi estudado na parte teórica, item 2.1, quando uma partícula com carga elétrica
penetra em um campo indução magnético, ela sofre uma força lateral e, como consequência, ela passa a executar
um movimento circular. Para determinar o raio do círculo, devemos usar a eq. 74-05. Para
maior clareza vamos reproduzir a eq. 74-05, abaixo:
Substituindo pelos valores numéricos dados pelo enunciado do problema, temos
Efetuando o cálculo encontramos o raio do círculo, ou
Devemos determinar se a trajetória da partícula vai ser desviada para a esquerda ou direita.
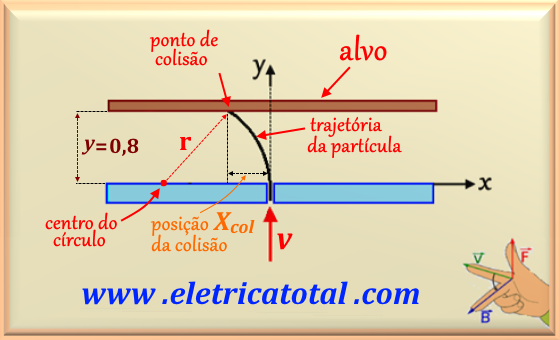
Usando a regra da mão direita (veja posição da mão na Figura 74-01.2) facilmente percebemos
que a partícula será desviada para a esquerda. Note que estabelecemos um referencial x-y.
Como a trajetória é um círculo, e o raio do círculo é r = 1 m, usando a equação do círculo
vamos conseguir determinar a posição x da colisão, pois já sabemos que a posição y
da colisão acontece em y = 0,8 m. Então:
Efetuando o cálculo, encontramos
Agora, preste atenção ao fato que o valor encontrado de x é em referência ao centro do círculo.
Mas o enunciado do problema pede a distância da colisão em referência
ao orifício do anteparo. Logo, essa distância será:
Logo, podemos afirmar que no referencial x-y a colisão com o alvo acontecerá em (-0,4 m; 0,8 m).
Veja o diagrama solicitado na Figura 74-01.2.