Problema 83-3    Fonte:  Problema elaborado pelo autor do site.

No circuito mostrado na Figura 83-03.1, assumindo uma sequência direta, temos:

V_AN = 127 ∠0° e Z_AB = Z_BC = Z_CA = 15∠-60°. Calcule:

a) as tensões de linha e suas respectivas fases.

b) as correntes de fase e linha.

c) a potência ativa dissipada pelo circuito.

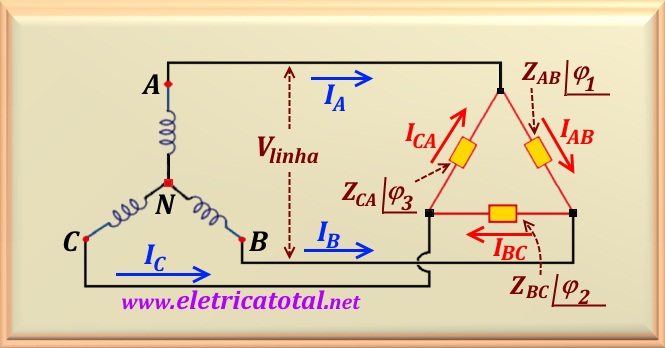
Solução do Problema 83-3

Item a

Como foi fornecida a tensão de fase, V_AN, então pelo diagrama mostrado na Figura 83-03.2 se percebe que V_AB deve estar adiantada de 30° em relação à V_AN. Por consequência, V_BC deve estar atrasada de 120° em relação à V_AB e V_CA deve estar adiantada de 120° em relação à V_AB. E assim, as tensões de linha estão perfeitamente definidas. Não esquecendo que a magnitude deve ser multiplicada por √3. Logo:

Item b

Para se calcular as correntes de fase basta aplicar a lei de Ohm, ou:

Como se conhece as correntes de fase, facilmente se encontra as correntes de linha, basta usar a eq. 83-02 mostrada abaixo.

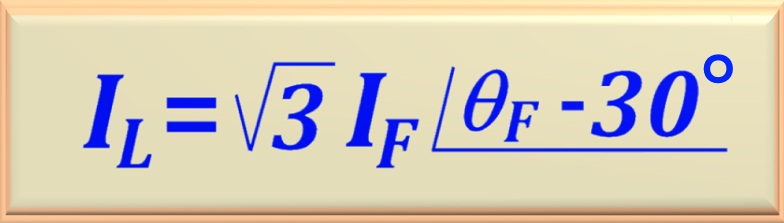
Logo, deve-se multiplicar a magnitude da corrente de fase por √3 e subtrair 30° do ângulo. Lembre-se que a corrente de linha A está associada à corrente de fase AB. Para as outras fases é o mesmo. Assim:

Uma outra maneira de calcular as corrente de linha é aplicar a lei de Kirchhoff para cada nó da ligação delta.

Item c

Para se calcular a potência ativa dissipada no circuito basta calcular a potência dissipada pelo resistor de cada fase e multiplicar o resultado por três, pois o circuito é equilibrado. Transformando o valor da impedância dada na forma polar para a forma cartesiana, descobre-se o valor do resistor. Assim Z_AB = 15∠-60° = 7,5 - j13. Logo, o valor do resistor é 7,5 Ω. Então:

Então a potência ativa total do circuito é: