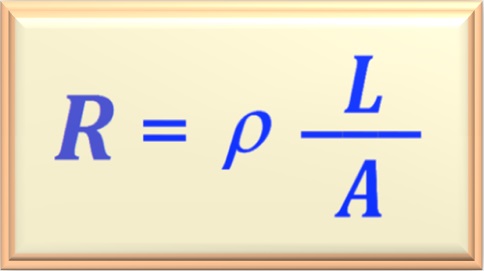Problema 73-5  Fonte:   Problema elaborado pelo autor do site.

Na Figura 73-05.1 vemos um cabo elétrico utilizado em linhas de transmissão de alta tensão. Repare no núcleo feito de um composto de carbono especial de raio a, sendo mais resistente e leve que o aço e não-condutivo. O material condutor é o alumínio com raio externo b. Este cabo tem uma corrente nominal de I = 1,00 kA.

a) Se a = 4,5 mm e b = 14,5 mm, encontre a densidade de corrente.

b) Calcule a razão Ω/Km do cabo.

c) Encontre a perda Joule do cabo por Km para a corrente nominal.

Solução do Problema 73-1   

Item a   

Para calcularmos a densidade de corrente devemos calcular a área do cabo. Portanto, calculamos a área do cabo considerando o raio externo b e depois subtraímos a área considerando o raio interno a. Logo:

Efetuando o cálculo encontramos o valor da área, ou

De posse desse dado e usando a eq. 73-06, calculamos a densidade de corrente, ou

Transformando esse valor para A/mm², vamos encontrar J = 1,67 A/mm². Comparando com a densidade de corrente utilizada em projetos de transformadores que pode variar de 1,50 a 3,00 A/mm², dependendo da utilização do transformador, percebemos que o valor encontrado para a linha de transmissão é um valor bastante pertinente.

Item b   

Para calcularmos a razão Ω/km devemos conhecer a resistividade do alumínio. Consultando a Tabela 02-1 no Capítulo 2, temos que ρ = 2,75 x 10^-8 Ω . m. Portanto, vamos usar a eq. 02-01 para calcular a resistência elétrica do cabo quando seu comprimento é L = 1.000 m. Abaixo reproduzimos a eq. 02-01, para maior clareza.