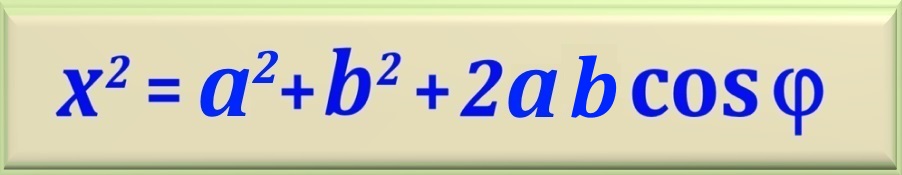Problema 71-2    Fonte:  Problema elaborado pelo autor do site.

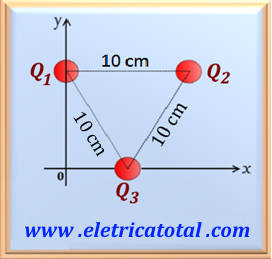
Vemos na Figura 71-02.1 a distribuição de três partículas, Q₁, Q₂ e Q₃, no plano x-y. Se as três partículas possuem a mesma carga, sendo igual a + 5 µC, calcule a força, em módulo, direção e sentido, que a partícula Q₃ sofre em presença das outras duas.

Solução do Problema 71-2   

Como todas as partículas possuem cargas de mesma polaridade, então as forças serão de repulsão. Para o cálculo do módulo das forças, vamos usar a eq. 71-04, estudada no item 3 do capítulo 71 e repetida aqui para maior clareza.

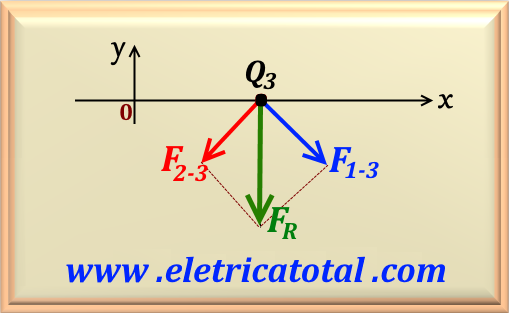
Vamos calcular a força que a partícula Q₁ exerce sobre a partícula Q₃, representando esta força por F_1-3. Lembrando que K = 9 x 10⁹ N . m² / C². Assim

Efetuando o cálculo encontramos o módulo da força, ou

Como as partículas Q₁ e Q₂, encontram-se à mesma distância da partícula Q₃, então os valores dos módulos das duas forças serão iguais. Muda apenas a direção e sentido conforme podemos ver na Figura 71-02.2.

Note que para encontrarmos o valor da força resultante sobre a partícula Q₃, devemos somar vetorialmente as forças F_1-3 e F_2-3. Porém, da Figura 71-02.1 percebemos que o ângulo entre essas duas forças é igual a 60°, pois as três partículas estão situadas nos vértices de um triângulo equilátero. Então podemos calcular o valor da força resultante utilizando a eq. 51-02, estudada no capítulo 51 e vamos repeti-la aqui para recordarmos uma equação muito importante.

Nesta equação, temos que x = F_R, a = F_1-3, b = F_2-3 e φ = 60°. Logo, fazendo a substituição numérica e efetuando o cálculo, obtemos:

Esse é o módulo da força resultante. Quanto à direção e sentido podemos ver pela Figura 71-02.1 que tem direção e sentido do eixo-y negativo. Vetorialmente, podemos escrevê-la como