Problema + Difícil 58-2
Fuente: Problema elaborado por el autor del sitio web.
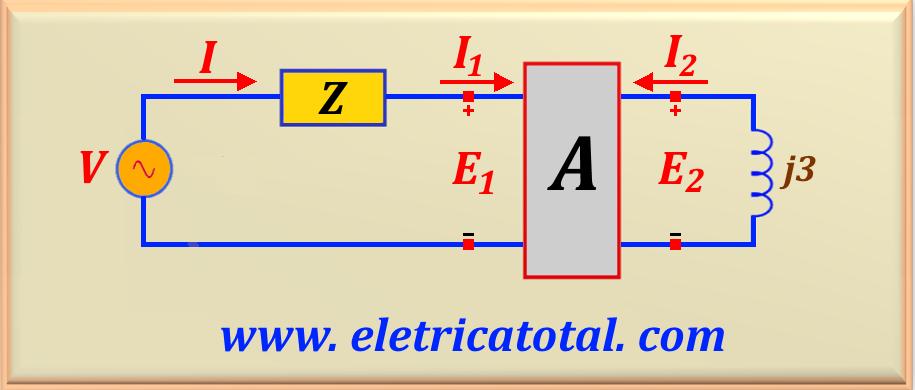
Dadas las ecuaciones de cuadrupolo A a continuación, determine Z de modo que I sea máximo.
Solución del Problema + Difícil 58-2
Debemos tener en cuenta que como el problema requiere que la corriente I sea máxima, esto implica que el circuito debe ser un circuito resonante en serie. En este caso, la corriente I debe ser igual a I1 en magnitud y dirección. Mirando el lado derecho del cuadripolo podemos escribir:
Este valor se puede sustituir en la ecuación ⓶. Pronto:
Esta igualdad se puede sustituir en ⓵, encontrando:
Tenga en cuenta que encontramos una relación entre E1 y I1, por lo que esto nos permite encontrar la impedancia equivalente del circuito a la derecha de la impedancia Z.
Para finalizar la solución al problema, hagamos algunas consideraciones. Consideremos Z = R ± j X. Para que el circuito esté en resonancia
la impedancia total del circuito debe ser un número real. Por lo tanto, Z se reduce a Z = R - j10. Sin embargo, como el planteamiento del problema requiere que la corriente sea máxima, entonces R = 0. Por lo tanto: